The operation of a cyclotron is based on the fact that the period of the motion of a charged particle in a uniform magnetic field is independent of the velocity of the particle, as can be seen in the following derivation:
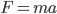

Solve for  :
:

Now find the period, 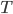 :
:
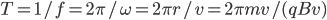
The  's cancel:
's cancel:

The 'Cyclotron Frequency'  immediately follows:
immediately follows:
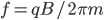
Fig. 1 is a schematic drawing of a cyclotron. The particles move in two semicircular metal containers called DEEs (because of their shape). The dees are housed in a vacuum chamber that is in a uniform magnetic field provided by an electromagnet. (The region in which the particles move must be evacuated so that the particles will not lose energy and be scattered in collisions with air molecules.) Between the dees there is maintained a potential difference  that alternates in time with a period
that alternates in time with a period 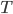 , which is chosen to be equal to the cyclotron period that was found in the above derivation. This potential difference creates an electric field across the gap between the dees. At the same time, there is no electric field within each dee because of the shielding of the metal dees.
, which is chosen to be equal to the cyclotron period that was found in the above derivation. This potential difference creates an electric field across the gap between the dees. At the same time, there is no electric field within each dee because of the shielding of the metal dees.
The charged particles are initially injected into dee 1 with a small velocity from an ion source near the center of the dees. They move in a semicircle in dee 1 and arrive a the gap between dee 1 and dee 2 after time 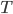 , where
, where 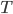 is the cyclotron period, and is also the period with which the potential across the dees is alternated. The alternation of the potential is adjusted so that dee 1 is at a higher potential than dee 2 when the particles arrive at the gap between them. Each particle is therefore accelerated across the gap by the electric field across the gap and gains energy equal to q. Because it has more kinetic energy, the particle moves in a semicircle of larger radius in dee 2, and again arrives at the gap after a time
is the cyclotron period, and is also the period with which the potential across the dees is alternated. The alternation of the potential is adjusted so that dee 1 is at a higher potential than dee 2 when the particles arrive at the gap between them. Each particle is therefore accelerated across the gap by the electric field across the gap and gains energy equal to q. Because it has more kinetic energy, the particle moves in a semicircle of larger radius in dee 2, and again arrives at the gap after a time 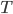 . By this time the potential between the dees has been reversed so that dee 2 is now at the higher potential. Once more the particle is accelerated across the gap and gains additional kinetic energy equal to
. By this time the potential between the dees has been reversed so that dee 2 is now at the higher potential. Once more the particle is accelerated across the gap and gains additional kinetic energy equal to  . Each time the particle arrives at the gap, it is accelerated and gains kinetic energy
. Each time the particle arrives at the gap, it is accelerated and gains kinetic energy  . Thus, it moves in larger and larger semicircular orbits until it eventually leaves the magnetic field. In the typical cyclotron, each particle may make up to 50 to 100 revolutions before reaching its final energy.
. Thus, it moves in larger and larger semicircular orbits until it eventually leaves the magnetic field. In the typical cyclotron, each particle may make up to 50 to 100 revolutions before reaching its final energy.
The kinetic energy of a particle leaving a cyclotron can be calculated by the following derivation:
1st set the following equal to the  of the dees and solve for the particle's velocity:
of the dees and solve for the particle's velocity:


Next solve for the Kinetic Energy:

Cancel the  's and finally get:
's and finally get:

Now for an example with the Rutgers 12-Inch Cyclotron running protons, determine the cyclotron frequency and maximum Kinetic Energy:
12-INCH CYCLOTRON PARAMETERS:
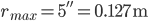
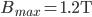


1st Determine the Cyclotron Frequency:

2nd Find the maximum Kinetic Energy of the protons:
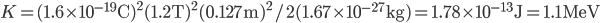
- adapted from Tipler's Physics for Scientists and Engineers, Vol. 2.
